| Secciones |
|---|
| Foros Electrónica |
|
|
| Boletines de correo |
 |
| Alguien dijo ... |
| Que la comida sea tu alimento y el alimento tu medicina, Hipócrates(s. V AC- s. IV AC) Médico griego. |
| Contacto |
Ley de Ohm
En los terminales de una batería existe la fuerza electromotriz (FEM) cuando no se toma corriente. Esta fuerza electromotriz, es considerada en ocasiones como una presión eléctrica y se debe a un sobrante de electrones en uno de los terminales, y a la falta de electrones en la otra. El sobrante y la falta de electrones, es causado por la acción química de la batería. En tanto por un lado exista exceso y por la otra falta de electrones habrá una atracción entre las cargas.
En el momento oportuno, el exceso de electrones del terminal negativo se precipitará para combinarse con los átomos deficientes de electrones en el terminal positivo y se considera que dichos electrones están bajo presión. Pregunta: ¿Porqué los electrones no pasan por la batería y se combinan con los iones positivos(átomos deficientes de electrones)? Porque los electrones y los iones se generan bajo presión y no pueden volver a la batería tanto como el agua que no puede retroceder a la bomba para igualar la presión creada por la misma. Así como el agua fluye por tuberías exteriores para neutralizar la presión de la bomba, también los electrones fluyen por los conductores para neutralizar los iones.
Al recorrido que ofrecen los conductores a la corriente de la batería se le llama circuito. Cuando se conectan uno más conductores a la batería, pero sin completar el recorrido para que circulen los electrones, se le llama circuito abierto, por el contrario, si se completa el camino se le llama circuito cerrado, estos términos se aplican a cualquier fuente de fuerza electromotriz
Cuando se conecta un conductor al terminal negativo de una fuente de fuerza electromotriz, el exceso de electrones se distribuye por sí mismo a los largo del conductor, y cuando se conecta al terminal positivo, los átomos se ionizan en el conductor, aunque el circuito no se complete(se cierre) los extremos de los conductores tienen exceso o falta de electrones. Si se aplica una fuente de fuerza electromotriz mayor la ionización será más completa.
La relación entre corriente y voltaje es un hecho, imaginemos nuevamente el circuito abierto. Si a una batería le conectamos un voltímetro(en paralelo con los terminales de la batería), un interruptor, un amperímetro(en serie con el circuito) y una resistencia, creamos un circuito(abierto). En este caso el voltímetro indicará el voltaje de la batería, aún con el circuito abierto, en cambio el amperímetro indicará cero puesto que no circula corriente por el circuito, en tanto exista una diferencia de cargas en los terminales de la batería, existe un voltaje, esto puede definirse como una diferencia de potencial.
Ahora, cerramos el interruptor, lo cual nos da un circuito cerrado, el voltímetro seguirá indicando el voltaje y el voltaje en el interruptor será "0"; en este caso el amperímetro indicará la corriente que fluye por el circuito, obviamente cuando cerramos el circuito el voltaje tendrá una ligera caída por efecto de la resistencia interna de la batería, en algunos casos esta caída será insignificante.
Cuando los electrones circulan por la resistencia tratan de agruparse en el lado por donde entran, esto significa que existen más electrones en el lado de la resistencia por donde entran, que por el lado donde salen existiendo en la resistencia un voltaje. La polaridad del voltaje a través la resistencia se contrapone a la polaridad de la batería, dicho de otra manera, el voltaje en la resistencia se opone al voltaje de la batería, esto obedece a que el voltaje negativo de la resistencia trata de rechazar a los electrones de la batería. dado que el voltaje en la resistencia se establece por la circulación de corriente, no es posible para ese voltaje detener la circulación de corriente, si esto fuera posible, el voltaje en la resistencia sería "0" y la corriente de la batería no tendría oposición. Si medimos el voltaje de la resistencia, el voltímetro indicaría exactamente el mismo que en los terminales de la batería.
RELACION ENTRE VOLTAJE, CORRIENTE Y RESISTENCIA:
Si se aplican 10 voltios a una resistencia de un ohmio en un circuito cerrado, fluye por el una corriente de 10 amperios los cuales se pueden medir con un amperímetro. La caída de voltaje en la resistencia es de 10 voltios, medidos con un voltímetro y es opuesto en polaridad al voltaje de la batería.
Si se aumenta el voltaje a 20 y la resistencia sigue siendo de 1 ohmio, esto es causa de una corriente de 20 amperios, mismos que fluirán por la resistencia. La caída de voltaje en la resistencia sigue siendo igual al voltaje de la batería, en este caso 20 voltios.
Otro ejemplo: Si mantenemos el voltaje en 20 voltios y aumentamos la resistencia a 5 ohmios, la corriente bajará a 4 amperios. A esta relación entre el voltaje, la corriente y la resistencia se le llama "LEY DE OHM".
LEY DE OHM:
En la ciencia, para producir un efecto debe existir una causa y como consecuencia, para producir un efecto la causa debe vencer la oposición presente. En electricidad esta regla se demuestra; la fuerza electromotriz es la causa, la corriente es el efecto y la oposición es la resistencia. La relación entre voltaje, corriente y resistencia se compara por analogía con un circuito eléctrico y uno hidráulico. Cuando se aumenta la fuerza electromotriz, se aumenta la corriente, entonces se dice que la corriente es directamente proporcional al voltaje(FEM), si aumentamos al doble el voltaje la corriente crecerá también el doble. También la corriente es inversamente proporcional a la resistencia, en este caso, si la resistencia se hace mayor, la corriente se hará menor.
Como se dio el ejemplo anteriormente, cuando la resistencia se aumento 5 veces la corriente bajo a una quinta parte. Resumiendo, decimos que la corriente es directamente proporcional al voltaje e inversamente proporcional a la resistencia, esta relación se expresa en la ecuación matemática siguiente:
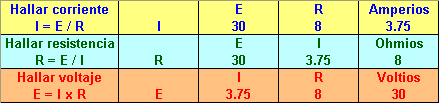
I (corriente o amperaje) es igual a E (voltaje) dividido R (resistencia en ohmios).
Esta relación se conoce como ley de ohm porque fue desarrolada por el físico alemán Georg Simón Ohm ( 1787 - 1854 ). Esta ecuación fue hallada en el año de 1,827.
La ecuación anteriormente descrita nos sirve para hallar la corriente, si el voltaje y la resistencia se conocen, tomemos como ejemplo que tenemos 20 voltios ( E ) y un resistor de 5 ohmios ( R ) el resultado es 4 amperios ( I ). Si lo que queremos es hallar la resistencia, la ecuación es: R igual a E dividido I, o sea, 20 voltios dividido 4 amperios igual: 5 ohmios.
Ahora bien, lo que queremos es hallar el voltaje, aquí usamos la ecuación siguiente:
E igual a I por R, o sea: 4 amperios por 5 ohmios igual: 20 voltios.

El amperio se puede sub - dividir en: miliamperios(milésima parte de un amperio) y en microamperios(millonésima parte de un amperio). Los miliamperios se utilizan en la mayoría de los circuitos transistorizados. Los símbolos para miliamperios y microamperios son como siguen respectivamente: mA - uA.
La resistencia es expresada en ohmios, un ohmio es la resistencia que presenta un circuito X donde un voltio hace circular un amperio de corriente. La otra forma de definir un ohmio está r una columna de mercurio puro de una sección transversal (grueso) de un milímetro cuadrado y de 106.3 centímetros de largo, a la temperatura de cero grados centígrados. En ohmio es muy pequeño para muchas mediciones en electrónica, por lo mismo en algunas resistencias se utilizan las palabras kilo (1000 ) y Mega ( 1,000,000 ). Además se utiliza un código de colores para identificar el valor de estas, ya que un valor muy grande no cabría en el cuerpo de la resistencia, por ejemplo una resistencia de 1,000,000 ohmios (1 Mega-ohmio)tendría los colores: marrón - negro - verde.
CIRCUITOS EN SERIE:
Hasta aquí se han hecho cálculos con una resistencia conectada en los terminales de la batería, en este caso nos preguntamos, ¿si hay más de una resistencia, como se aplica la ley de ohm?. Hay 3 maneras de conectar un resistor a un circuito: en serie, en paralelo y en serie - paralelo. Cada uno de estos métodos de conexión se usa en la práctica y depende del resultado deseado. En esta oportunidad se hablará del circuito en serie, cuando hablamos de un circuito en serie significa que las resistencias u otros componentes se conectan uno tras otro, para decirlo de otra forma, en fila.
En la figura inferior se pueden ver 3 resistencias en serie conectados a una batería. En este caso la corriente que circula por una resistencia en serie debe circular por todos los demás, definido de esta forma se obtiene una regla importante: LA CORRIENTE DE TODAS LAS PARTES DE UN CIRCUITO EN SERIE ES IGUAL. Si se coloca un amperímetro entre R1 y R2, o bien R2 y R3, o entre la batería y R1, el instrumento indicará el mismo amperaje.
Como ya se dijo, la corriente eléctrica se mide en electrones por segundo, la corriente será siempre la misma en cualquier parte del circuito; aún puede existir alguna duda del lado por donde entran los electrones en la resistencia. Dada la oposición de la resistencia, los electrones se acumularán y su paso será lento, por lo mismo la proporción de la circulación de estos es la misma cantidad de electrones por segundo. En la figura se puede observar que la resistencia total(Rt) es igual a: 500 + 200 + 300 = 1000 ohmios. La corriente que circula y que está limitada por la resistencia total, según la ley de ohm, deducimos: I = E dividido Rt = 100 dividido 1000 = a 0.1 amperio. Esta es la corriente que circula en cada resistencia, Como cada resistencia tiene diferente valor, el voltaje en cada uno es diferente. En los siguiente cálculos se notará que se usa el símbolo "V" que equivale a la caída de voltaje, en otras palabras "E" lo definimos como el voltaje de la fuente(batería) y "V", como la caída de voltaje.
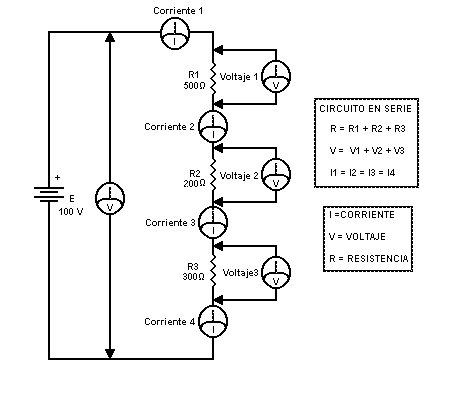

Si observan los cálculos, notaremos que, aunque son diferentes los voltajes en cada resistencia, la suma de los voltajes de caída es igual al voltaje aplicado(E), ahora veamoslo en una ecuación matemática: E = V1 + V2 + V3, en números: 50 + 20 + 30 = 100 voltios.
CIRCUITOS EN PARALELO
Se ha explicado ya el cálculo de los circuitos en serie, ahora se hablará sobre los circuitos en paralelo, en estos como se podrá notar que existen algunas variantes con respecto a los circuitos en serie.
En la figura se puede observar un circuito con 2 resistencias en paralelo. Los electrones que parten de la batería se dividen en 2 grupos, uno de los cuales circula por R1 y el otro por R2 pero, los 2 grupos se juntan nuevamente al otro extremo de la unión y regresan a la batería. Dado que existen caminos paralelos para la circulación de la corriente, la combinación de resistencias de dicha figura se llama circuito paralelo.
Como puede notarse en este circuito, ambas resistencias se conectan directamente a los terminales de la batería, y la teoría indica que no existe resistencia en los alambres conductores. Para estos circuitos existe la regla: EL VOLTAJE EN TODAS LAS PARTES DE UN CIRCUITO EN PARALELO ES EL MISMO. La corriente en R1 puede encontrarse por la ley de ohm. Ya que dicha corriente es diferente de la corriente en R2.


El último cálculo está basado en una importante ley. La corriente total (It) se encontró sumando las corrientes en cada ramal, esto hace pensar que no puede circular más corriente de la que entrega la batería, esto está expresado en una ley fundamental que se conoce como LEY DE KIRCHHOFF, misma que determina que LA SUMA DE LAS CORRIENTES QUE ENTRAN A UN PUNTO ES IGUAL A LA SUMA DE LAS CORRIENTES QUE SALEN DE DICHO PUNTO. Por lo mismo, la corriente total que circula por las 2 resistencias en paralelo es de 1.5 amperios. Puede conectarse una sola resistencia en los terminales de la batería lo que causa que circule el mismo valor de corriente; ¿que valor tendrá esta resistencia?. Tanto la corriente (1.5 A) como el voltaje (10 V) se conocen, aquí aplicamos la ecuación: R = E dividido I, o sea, 10 dividido 1.5 igual 6.66 ohmios, esto quiere decir que este valor es equivalente a las 2 resistencias de la figura ya que por este también circulan 1.5 amperios, de este hecho se deriva su nombre: Resistencia equivalente (Req), abajo se indica como obtener directamente la resistencia equivalente

Como puede notarse, aquí también el valor de la resistencia es 6.66 ohmios. Ya se sabe como encontrar el valor equivalente de 2 resistencias en paralelo, lo que se verá en adelante es como se encuentra este valor de 3 o más resistencias en paralelo. En el caso de encontrar la resistencia total de 2 o más resistencias en serie, fue solo sumar el valor de cada una; para una combinación en paralelo, esto se calcula de diferente forma dado que la resistencia equivalente resulta siempre menor que el valor más bajo de combinación en paralelo. Las dos fórmulas empleadas para las 2 resistencias en paralelo se aplican para 3 o más resistencias, siendo necesaria una pequeña modificación en el procedimiento para usar la fórmula de la resistencia equivalente. Se demostrará nuevamente los 2 métodos.
En la figura se observa un circuito con un voltaje de 80 voltios, el cual circula por las 3 resistencias, ahora se debe encontrar la corriente que circula por cada una de ellas, veamos las fórmulas:


Como puede notarse la resistencia equivalente es de menor valor que la resistencias de menor valor de la combinación de resistencias. Al aplicar la fórmula para resistencias en paralelo se debe recordar que sirve solamente para 2 resistencias únicamente; por lo mismo, R2 y R3 pueden ser subsituidas en la fórmula y encontrar la resistencia equivalente de las 2. Dicha resistencia equivalente puede luego combinarse con R1 para encontrar la resistencia de la combinación. Por supuesto que, R1 se puede combinar primero con R2, y la resistencia equivalente del par se combina con R3, o se pueden combinar primero R1 y R3 y la resistencia que resulte como equivalente se combina con R2; de cualquier manera, el resultado sera el mismo. Veamos un ejemplo: R1eq = R2 X R3 dividido R2 + R3, que es lo mismo, "0 X 40 dividido 20 + 40 = 800 dividido 60 = 13.3 ohmios.
No hay que confundir Req con R1eq, en este caso se refiere a encontrar la resistencia equivalente de R2 y R3. Req = R1 X R1eq dividido R1 + R1eq = 10 X 13.3 dividido 10 + 13.3 = 133 dividido 23.3 = 5.7 ohmios. El resultado es el mismo obtenido por el método directo.
Por lo general no todos los resultados coinciden exactamente como se ha descrito, esto se debe al hecho de que la operación se forzó nada más que hasta una fracción decimal, y para demostrarlo, se puede forzar la operación de arriba para obtener tres lugares después del punto decimal lo que cambiaría ligeramente el resultado. Normalmente se efectúan las operaciones hasta conseguir los 3 lugares para las fracciones.
Si se diera el caso que dos o más resistencias están conectadas en paralelo pero no se conoce el voltaje, se puede suponer sin que importe el voltaje que se suponga.
Cuando se calcule la corriente resulta de un valor X, que, dividiendo el voltaje entre la corriente dará el valor de la resistencia. Lo cual se puede demostrar cambiando el voltaje aplicado a 100 voltios en el problema que recién se resolvió y usando el método indirecto para la resistencia. El valor de la resistencia obtenido será el mismo (5.7 ohmios).
CIRCUITOS SERIE - PARALELO
En la práctica de electrónica nos encontraremos que las resistencias no siempre se conectarán en serie o en paralelo únicamente, también se conectarán en una combinación de estos o sea, serie - paralelo. En la figura se muestra un circuito de este tipo. Para el cálculo de un circuito serie - paralelo, la combinación el paralelo se substituye con la resistencia equivalente (Req), luego el circuito se convierte en simples resistencias en serie cuyo valor óhmico se puede encontrar con una simple suma de ellas.







