Parametros de la corriente alterna
Ya hemos visto los componentes pasivos y su comportamiento en corriente continua. Dado que el comportamiento de éstos varía al tratarlos en corriente continua o corriente alterna merece un párrafo aparte la discusión sobre el comportamiento de estos elementos cuando se los somete a la circulación de una corriente alternada.Antes de comenzar conviene remarcar la diferencia de este tipo de corriente con la corriente continua y también la explicación de los parámetros mas importantes de una señal alterna.La corriente continua es aquella que mantiene su valor de tensión constante y sin cambio de polaridad, ejemplo de ella puede ser una batería de las que se utilizan en los automóviles o las pilas con las que alimentamos nuestros juguetes o calculadoras electrónicas. A este tipo de corriente se la conoce como C.C. o, según los autores de habla inglesa, D.C.
La corriente alterna también mantiene una diferencia de potencial constante, pero su polaridad varía con el tiempo. Se la suele denominar C.A. o A.C. en inglés.
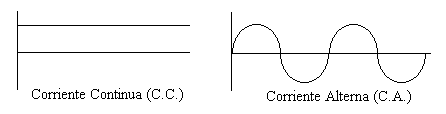
Parámetros
Frecuencia: Número de veces que una corriente alterna cambia de polaridad en 1 segundo. La unidad de medida es el Hertz (Hz) y se la designa con la letra F. De esta forma si en nuestro hogar tenemos una tensión de 220 V 50 Hz, significa que dicha tensión habrá de cambiar su polaridad 50 veces por segundo.Una definición más rigurosa para la frecuencia: Número de ciclos completos de C.A. que ocurren en la unidad de tiempo.
Fase: Es la fracción de ciclo transcurrido desde el inicio del mismo, su símbolo es la letra griega q.Período: Es el tiempo que tarda en producirse un ciclo de C.A. completo se denomina T. En nuestro ejemplo de una tensión de 220 V 50 Hz su período es de 20 mseg.La relación entre la frecuencia y el período es F=1/T
Valor instantáneo: Valor que toma la tensión en cada instante de tiempo.
Valor máximo: Valor de la tensión en cada "cresta" o "valle" de la señal.
Valor medio: Media aritmética de todos los valores instantáneos de la señal en un período dado.Su cálculo matemático se hace con la fórmula:
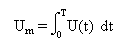
Valor eficaz: Valor que produce el mismo efecto que la señal C.C. equivalente. Se calcula mediante:
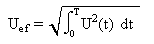
Valor pico a pico: Valor de tensión que va desde el máximo al mínimo o de una "cresta" a un "valle".En las siguientes figuras vemos una señal alterna donde se han especificado algunos de estos parámetros, la figura a) muestra una onda alterna donde se ven tanto el valor eficaz, el valor máximo, el valor pico a pico y el período. En la figura b) vemos dos ondas alternas, de igual frecuencia, pero desfasadas 90º.
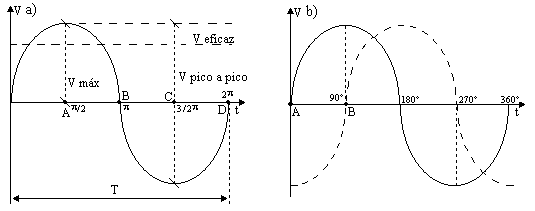
En la figura a) si la frecuencia es de 50 Hz entonces el período es T=20 mseg y abarcará desde el origen hasta el punto D. En ella también se puede ver la fase, la que es medida en unidades angulares, ya sea en grados o radianes. También podemos ver los distintos puntos donde la señal corta al eje del tiempo graduado en radianes.En la figura b), como ya lo dijimos, se ven dos señales alternas desfasadas 90º (p/2 radianes), esto es, cuando la primera señal arranca del punto A, la segunda lo hace desde el punto B, siendo el desfasaje entre los puntos A y B de 90º. Por lo tanto se dice que tenemos dos señales de igual frecuencia y amplitud pero desfasadas entre sí por 90º.Con lo visto hasta ahora estamos en condiciones de presentar a una señal senoidal en su representación típica:
U = Umax sen (2pft + q)
Donde:
- Umax: tensión máxima
- f: frecuencia de la onda
- t: tiempo
- q: fase
Otros tipos de corriente alterna:
En electrónica se utilizan infinidad de tipos de señales por lo cual se hace prácticamente imposible enumerarlas a todas, pero haremos referencia a las más comunes, luego de senoidal y la continua pura.Una de ellas es la pulsatoria (también llamada onda cuadrada). Esta onda se ve en la figura siguiente:
Otra onda frecuentemente utilizada en electrónica es la onda triangular:
y también está la onda diente de sierra:
Cabe aclarar que las definiciones de los parámetros que se hicieron para una onda senoidal se mantienen válidos para estos tipos de ondas.
Comportamiento de los componentes pasivos en C.A:
Los componentes pasivos tienen distinto comportamiento cuando se les aplican dos corrientes de distinta naturaleza, una alterna y la otra continua.La respuesta en C.C. ya la analizamos, nos resta analizar la respuesta de estos elementos en C.A.
Resistencias y C.A:
Estos son los únicos elementos pasivos para los cuales la respuesta es la misma tanto para C. A. como para C.C.
Se dice que en una resistencia la tensión y la corriente están en fase.
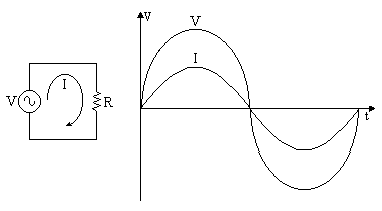
Inductancia y C.A.:
A este tipo de componente no hemos hecho referencia cuando tratamos a los elementos en C.C. dado su similar comportamiento a las resistencias en ese tipo de corriente. En cambio en C.A. su respuesta varía considerablemente

Las señales tensión y corriente mantienen la misma forma de onda pero ya no están en fase sino que desfasadas 90º. La corriente atrasa 90º con respecto a la tensión.El parámetro que mide el valor de la inductancia es la reactancia inductiva:
XL = 2 p f L donde XL se expresa en ohms
y como XL = V/I por la Ley de Ohm entonces tenemos que:
i(t) = V(t)/XL = V(t)/2pfL
Donde podemos ver que ahora la corriente no depende exclusivamente del valor de la tensión y de la reactancia inductiva, sino también de la frecuencia, siendo inversamente proporcional a esta.
Capacidad y C.A:
En la figura vemos la conexión de una capacidad a un circuito de C.A.

Es ahora el caso en el que la corriente se adelanta 90º con respecto a la tensión, manteniendo la misma forma de onda que ésta.El cálculo de la reactancia capacitiva (medida en ohms) se hace con la siguiente fórmula:
XC = ½pfC
y aplicando nuevamente la Ley de Ohm:
i(t) = V(t) / XC = 2pfC V(t)
También aquí la corriente depende de la frecuencia, pero ahora es directamente proporcional a ésta.
Impedancia:
Un factor que aparece en alterna es la impedancia. Esta se mide en ohms y se define:
Z = R + j(XL - XC)
Al ser un valor complejo (suma vectorial), se mide su módulo y fase:
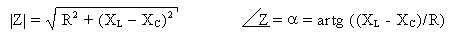
La inversa de la impedancia se denomina admitancia (Y) y se define:
Y = 1/Z
Combinaciones R-L, R-C y RLC:
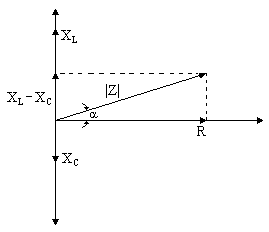
Además de los casos ya vistos donde solamente estaban presentes en un circuito un solo tipo de elemento pasivo, existen casos en los cuales se combinan resistencias con capacitores e inductancias, veremos cómo se comportan las corrientes y tensiones en cada una de estas combinaciones.R-L:
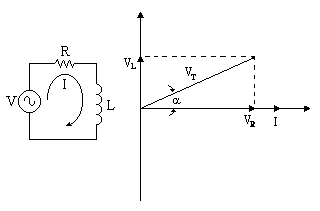
En la gráfica podemos ver el diagrama vectorial de las tensiones del circuito. Vemos cómo VR está en fase con la corriente, VL está adelantada 90º con respecto a esta y entonces resolviendo la suma vectorial vemos que VT está adelantada a grados a la corriente.R-C:

De la misma manera que en el circuito R-L vemos en el diagrama vectorial de las tensiones del circuito, como otra vez VR está en fase con la corriente, mientras que VC está 90º atrasada a la corriente. De la suma vectorial vemos que VT está a grados atrasada con respecto a I.R-L-C:
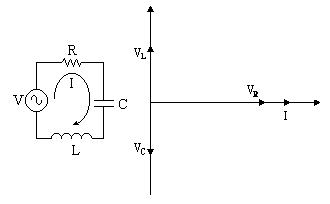
Por último veremos el caso en el que están presentes en un circuito de C.A. los 3 tipos de componentes pasivos (R, L, C).La impedancia (Z) se calcula como ya hemos visto.En el diagrama vectorial de las tensiones en el circuito vemos VC atrasada 90º a la corriente, VR en fase con ella y VL adelantada 90º. Nótese que en la figura no se dibujó la tensión resultante total dado que ésta será función de las tres tensiones presentes, resultando la tensión total (VT) adelantada a la corriente si XL > XC, atrasada si XC > XL y estará en fase con la corriente si XC = XL.







