|
| Autor | Mensaje |
|---|
| Asunto: confucion entre mapa de carnout y tabla incial de datos  Publicado: 29 Abr, 2009 - 04:46 Publicado: 29 Abr, 2009 - 04:46 |
| Nuevo en el Foro

Registrado: 29 Abr, 2009
Mensajes: 1
|
| saludos... soy nuevo en la parte de circuiteria, tengo un problema con una contradicciones... nos enviaron a hacer un diseño el cual representase por una salida si un numero de 4 bits (numero normal menor a 15 traducido en binario de 4 bits) es primo o no, recordemos que los números primos son aquellos que solo son divisibles para 1 y para si mismo.. dicho esto mi tabla quedo así
(n4,n3,n2,n1) =
(0 , 0, 0, 0) = 0
(0 , 0, 0, 1) = 1
(0 , 0, 1, 0) = 1
(0 , 0, 1, 1) = 0
(0 , 1, 0, 0) = 1
(0 , 1, 0, 1) = 0
(0 , 1, 1, 0) = 1
(0 , 1, 1, 1) = 0
(1 , 0, 0, 0) = 0
(1 , 0, 0, 1) = 0
(1 , 0, 1, 0) = 1
(1 , 0, 1, 1) = 0
(1 , 1, 0, 0) = 1
(1 , 1, 0, 1) = 0
(1 , 1, 1, 0) = 0
(1 , 1, 1, 1) = 0
y los números representados asta aqui donde la respuesta inicial el sistema son 1,2,5,7,11,13. asta aqui todo esta bien.. cuando traspaso los datos al mapa de carnot, y al extraer los implican tes primos me queda...
n4(negado).n1 + n1.n2(negado).n3 + n4(negado).n3(negado).n2 + n1.n2.n3(negado).
Y LA CONTRADICCIÓN QUE TENGO EN ESTE MOMENTO ES QUE SEGUN MI TABLA EL ELEMENTO (0 , 0, 1, 1) = 0 CONTRADICE A LO QUE DICE EL MAPA n1.n2.n3(negado)
ESA CONTRADICCIÓN ES VALIDA
ya e llevado los datos del mapa a un protoboard y es aquí donde me nació otra incógnita...
que es lo que se debe representar en el protoboard, los datos de la tabla o los datos del mapa...?
DE ANTEMANO AGRADEZCO SU AYUDA | |
| |
| |
| |  | | Asunto: hola  Publicado: 01 May, 2009 - 07:43 Publicado: 01 May, 2009 - 07:43 |
| Nuevo en el Foro

Registrado: 01 May, 2009
Mensajes: 1
|
| | en realidad no es una respuesta, resulta que tambien estoy estudiando y me han puesto este mismo ejercicio, y me gustaria que alguien nos ayudara, gracias..! | |
| |
| |
| |  | | Asunto:  Publicado: 03 May, 2009 - 01:09 Publicado: 03 May, 2009 - 01:09 |
| Vive en el foro

Registrado: 08 Jul, 2004
Mensajes: 253
Ubicación: Algorta (Vizcaya)
|
| Hola,¿estáis estudiando en el mismo sitio o los "profes" se copian los ejercicios? (es broma).
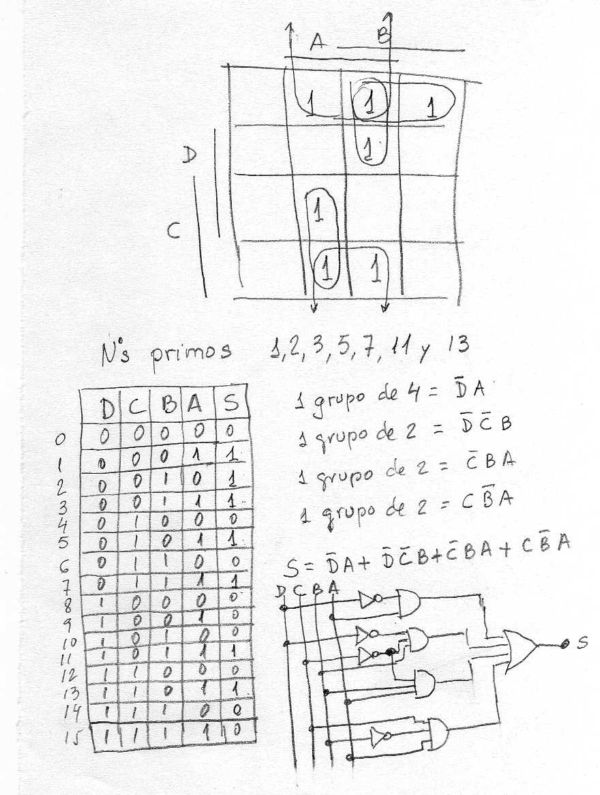
Aunque en la tabla de la verdad veo que tiene errores, curiosamente, las ecuaciones están bien y la presunta contradicción no existe, ya que la tabla debe dar salida 1 en la posición del Nº3 (0011=1) ya que es primo. Los mapas de Karnaugh (que tu le llamas carnot) se hacen con la única idea de simplificar la ecuación de salida, por lo tanto, siempre se utiliza la ecuación que resulta del mapa para hacer el circuito, que será más reducido que hacer la ecuación de la tabla que aún no está simplificada. Puede darse el caso de que no se obtenga ninguna simplificación en el mapa, en cuyo caso, el mapa no sirve para nada.Por cada grupo de dos unos que se obtiene en el mapa, desaparece una variable, en un grupo de 4 unos, desaparecen dos variable etc . He hecho el ejercicio a mano alzada, está un poco chapuza pero espero que lo podáis descifrar. Un saludo |
| MGB_Mapa de Karnaugh009.jpg |
|
| |
| |
| |  |
|
|
