Dominio Lógico
El funcionamiento del computador se basa en el dominio de las señales que se describieron en el ejemplo anterior, pero también un computador es mucho más complejo que aquellas señales, el sólo hecho de mirar la pantalla y ver la metáfora del mundo que aquella representa, hace surgir preguntas tales: ¿cómo funciona esto? O sí algo ya se sabe ¿cómo de un dominio tan pequeño, el de las señales, es posible obtener otro tan complejo como lo que se observa en la pantalla?
Para responder aquellas preguntas se debe partir desde el mismo dominio simple de los dos estado originales, el cual es posible representar por un conjunto de símbolos como { 0, 1 } o { V, F }, símbolos que describen a { -1.5 volts, +4.0 volts } respectivamente.
Pero se está frente a la misma situación anterior, sólo se ha cambiado la forma, pero ese conjunto de símbolos no tiene ninguna potencialidad, de ninguna forma es posible construir algo con aquellos símbolos.
Existe, en las matemáticas, un álgebra llamada Álgebra de Boole. Fue desarrollada originalmente por George Boole, alrededor de 1850. La importancia de esta álgebra deriva de los trabajos de Claude Shannon en 1937, quién la utiliza para describir los circuitos digitales.
Un álgebra es posible definirla, muy simplificadamente, como un dominio en que además de un conjunto de elementos existe un conjunto de operadores u operaciones que permiten operar con aquellos elementos, generando elementos del propio dominio o de otros.
Así, el Álgebra de Boole se describe como el siguiente dominio = ( { 0, 1 }, {And,Or,Not } ), donde el conjunto {And,Or,Not } corresponde al conjunto de operadores. Los símbolos con qué se representan estas operaciones son propios de esta visión simplificada del álgebra, ya que en el original son { ^, v, ~ } o desde el punto de vista del diseño de circuitos en ingeniería los símbolos que se utilizan son { ·, +, - }.
Otra propiedad de un Álgebra es la utilización de variables que permiten representar, en general, cualquiera de los elementos del conjunto. Esta característica permite definir nuevas operaciones a partir de las originales o primitivas del álgebra. Así, una variable X definida sobre le Álgebra de Boole puede tomar valores { 0, 1 }, por ejemplo X = 1, o X = 0. Para que sea más simple de entender se recomienda considerar 0 = falso y 1 = verdadero.
Operaciones Básicas And.
La operaciónAndrequiere que todas las señales sean simultáneamente verdaderas para que la salida sea verdadera. Así, el circuito de la figura necesita que ambos interruptores estén cerrados para que la luz encienda.
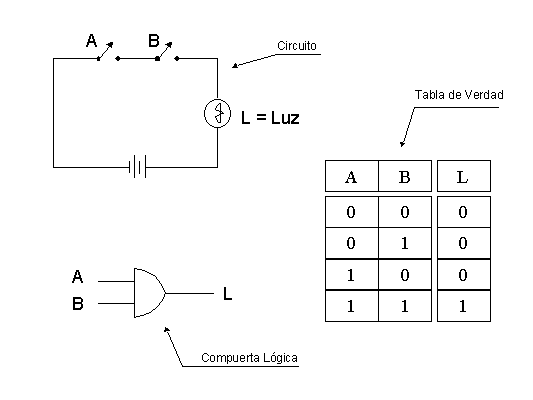
Figura No. 5. Operación And.
Los estados posibles del circuito se pueden modelar en la Tabla de Verdad que tiene asociada. Sabemos que los interruptores sólo pueden tener dos estados, abiertos o cerrados, si el interruptor abierto se representa mediante el cero (0 o falso) y el cerrado mediante el valor uno (1 o verdadero) entonces en la tabla de verdad asociada se puede ver la situación que se describía en el párrafo anterior, cuando se decía que la luz sólo prende cuando ambos interruptores están cerrados, es decir, si A = 1 y B = 1 entonces L = 1.
La compuerta lógica es una forma de representar la operación And pero en el ámbito de los circuitos electrónicos, para ese caso A y B son las señales de entrada (con valores = 0 1) y L es la señal de salida.
Para efectos de este curso, la operación And la representaremos como la función And( A, B ), donde A y B serían los parámetros de entrada (los mismos valores de A y B en el circuito) y L = And( A, B ), correspondería a la forma de asignación de valor a L. En este caso el parámetro de salida es la misma función And.
Operaciones Básicas Or.
La operación Or tiene similares características a la operación And, con la diferencia que basta que una señal sea verdadera para que la señal resultante sea verdadera. En la figura se puede ver tal situación.
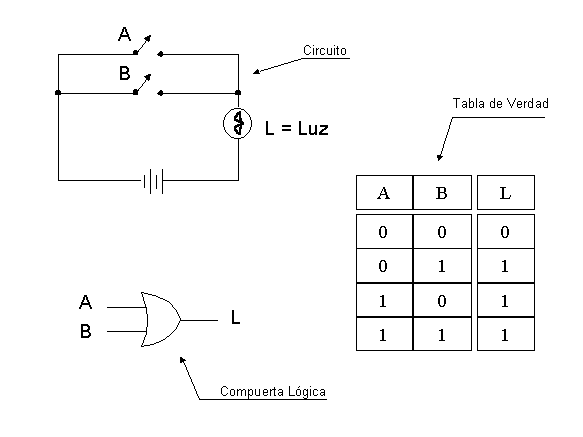
Figura No. 6. Operación Or.
Note que en el circuito los interruptores están en paralelo, por lo cual basta que uno de ellos esté cerrado para que el circuito se cierre y encienda la luz.
La operación Or también tiene una representación funcional como Or( A, B ) donde A y B serían los parámetros de entrada (los mismos valores de A y B en el circuito) y L = Or( A, B ), correspondería a la forma de asignación de valor a L. En este caso, el parámetro de salida es la misma función Or.
Not: La última de la tres operaciones fundamentales, la cual también se conoce como negación, complemento o inversión, es mucho más simple que las anteriores. En la figura se puede observar el circuito, que en este caso tiene la particularidad de que al estar el interruptor abierto la luz enciende, cuando él está en posición de cerrado la luz permanecería apagada.

Figura No. 7. Operación Not.
La notación funcional para esta operación será Not( A ), donde A corresponde a la señal de entrada y Not( A ) corresponde al valor complementario de A.
Con las operaciones básicas ya definidas es posible redefinir el Álgebra de una manera más formal, por ejemplo, dándole el nombre de Dominio Lógico y caracterizandolo de la siguiente manera:
Dominio Lógico ( lÎ Dominio Lógico ) = ( { 0, 1 }, { l: And( l, l ), l:Or( l, l ), l:Not( l ) } )
Note que cada una de las operaciones o funciones de este dominio se ha explicitado claramente la cantidad y el tipo de parámetros con los cuales ellas operan (operandos) y el tipo de valor que la operación devuelve, en este caso todos los parámetros son del tipo lógico ( l ).
Así, cuando se habla del dominio del computador al resolver un problema, este dominio tiene como base el dominio recién descrito. Los circuitos electrónicos que dan vida al computador pueden ser representados todos mediante este Dominio Lógico.







