| Secciones |
|---|
| Foros Electrónica |
|
|
| Boletines de correo |
 |
| Alguien dijo ... |
| El arte es yo; la ciencia es nosotros, Claude Bernard (1813-1878). Fisiólogo. |
| Contacto |
Teorema de Norton
El Teorema de Norton es el dual de Thévenin.
Tenemos una caja negra con fuentes, componentes lineales, etc, en las mismas hipótesis generales de Thévenin, y conectamos entre dos bornes una admitancia Y (es lo mismo que decir Z) sin mutua con el interior.
Trabajamos con la corriente de cortocircuito Icc y la admitancia vista YAB = 1/ ZAB
Norton dice que V = Icc/ (YAB + Y)
La demostración es análoga a la de Thévenin. Superponemos dos estados.
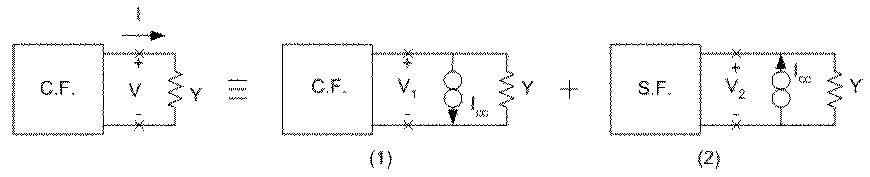
Digo que V1 = 0 es solución.
En efecto, si V1 = 0, la corriente por Y es cero, y por el sistema circula Icc, como al hacer el cortocircuito.
En el estado 2 , recordando la definición de admitancia vista; el bloque S.F. actúa como YAB
Luego: Icc = V2 (Y+YAB)
Como V = V1 + V2 = V2
V = (Icc/YAB +Y )
En otras palabras: el circuito se puede sustituir por su equivalente Norton:
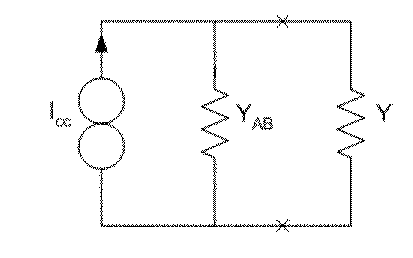
¿Cuál es la relación de éste con el equivalente Thévenin? El de Norton tiene la fuente de corriente en paralelo con la admitancia vista.
Ejemplo:
Los circuitos de Laplace con los datos previos.
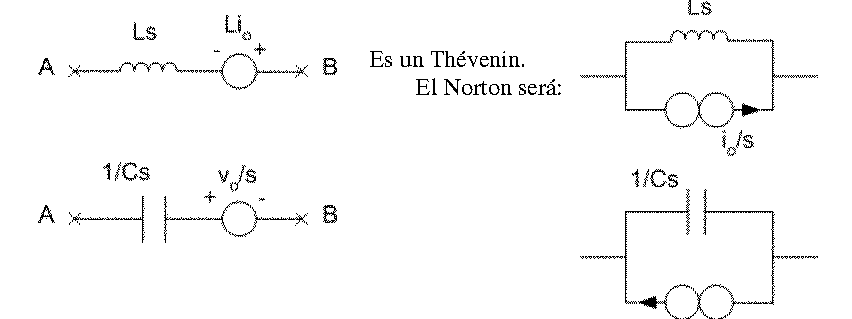
Ver que el sentido de la fuente Icc corresponde a salir por el + de VAB
Fuente cuasi ideal de tensión (ZAB<Z) y de corriente (ZAB>Z)
| Thévenin: V = ZVAB/(ZAB +Z) | Norton: I =YIcc/(YAB +Y ) |
| V = VAB ZAB<Z | I = Icc Þ YAB<Y |
| ZAB>Z |






